Chapitre 2 : Concepts fondamentaux de la modélisation multi-physique à paramètres localisés
5.1. Révision des lois de Kirchhoff en modélisation multi-domaine
1) Sur quelles grandeurs applique-t-on les lois des nœuds ?
La force $F$, le moment $T$, le courant $i$ , le flux $\dot{Q}$
2) Sur quelles grandeurs applique-t-on les lois des mailles ?
La vitesse $v$, la vitesse angulaire $ω$, la tension $v$, la température $θ$
3) Comment se distinguent ces deux types de grandeurs (across et through) dans le code des interfaces et lors de l’association des composants dans un modèle Modelica ?
Sur l’exemple d’un connecteur électrique, dans le code Modelica:
connector Pin "Pin of an electrical component"
SI.Voltage v "Potential at the pin";
flow SI.Current i "Current flowing into the pin";
end Pin;
La présence du préfixe « flow» permet de désigner la variable pour laquelle la loi des nœuds est appliquée.
L’absence du préfixe « flow » indique une variable pour laquelle la loi des mailles s’applique.
4) Quelle différence peut-on noter entre les domaines mécanique, électrique et le domaine thermique ?
Dans les domaines mécanique et électrique le produit des grandeurs tension/courant et effort/vitesse permettent de donner la puissance. Mais en thermique, le flux de chaleur est déjà une puissance.
5) Rappelez la notion de variables de puissance et de variables d’énergie utilisée par Modelica
Les variables de puissance sont les grandeurs nécessaires à la description des lois des nœuds et des mailles. Les variables d’énergie sont les grandeurs primitives des variables de puissance (ex : la charge électrique $q$, le flux magnétique $φ$)
6) Donnez les expressions des puissances dissipées ou des énergies stockées dans ces différents éléments
Pour un effet dissipatif :
- En mécanique translation : $ P=f.v^2 $
- En mécanique rotation : $P=d.ω^2$
-
En électricité : $P=R.I^2$
- Attention en thermique, le flux de chaleur est directement une puissance (provenant des autres domaines)
Pour un effet de stockage d’énergie de type “capacité” :
- En mécanique translation : $E=\dfrac{1}{2}k_t.z^2$
- En mécanique rotation : $E=\dfrac{1}{2}K_r.\theta^2$
-
En électricité : $E=\dfrac{1}{2}C.v^2$
- Attention en thermique : $E=C_{th}.\theta$, par intégration directe du flux de chaleur
Pour un effet de stockage d’énergie de type “inertie” :
- En mécanique translation : $E=\dfrac{1}{2}m.v^2$
- En mécanique rotation : $E=\dfrac{1}{2}J.\omega^2$
- En électricité : $E=\dfrac{1}{2}L.i^2$
7) Par analogie avec le reste du tableau, proposez une colonne pour le domaine hydraulique
Variable de puissance : Débit $Q_h~[m^3/s]$ et Pression $P~[Pa]$
Effet dissipatif : Résistance hydraulique en laminaire (faible débit) $\Delta P=R_h.Q_h$
Remarque: En turbulent (fort débit) la chute de pression est fonction du débit au carré.
Effet de stockage d’énergie (capacité) : Capacité hydraulique $Q_h=C_h.\dot{P}$
Effet de stockage d’énergie (inertie) : Inertance hydraulique $\Delta P=L_h.\dot{Q}_h$
5.2. Questions sur l’exemple du lève vitre
Ressources à télécharger : Modèle de simulation d’un lève vitre
Une modélisation du lève vitre est disponible : Chap2_PowerWindow.mo
1) Ecrivez les équations liant les variables électriques aux variables mécaniques
$v = Ri+L\frac{di}{dt}+k\Omega$
$J_{moteur}\frac{d\Omega}{dt} = k.i - T_{ch}$
2) Quelle loi de Kirchhoff s’applique à la liason réducteur / ressort de compensation / mécanisme ciseau ? Quel est l’intérêt du ressort de compensation ?
On applique ici la loi des noeuds : somme des couples égale à 0. Le ressort permet d’appliquer un couple qui compense l’effet du poids de la vitre. Le ressort permet ainsi de diminuer le couple à fournir par le moteur.
3) Indiquez ce que chaque composant Modelica modélise
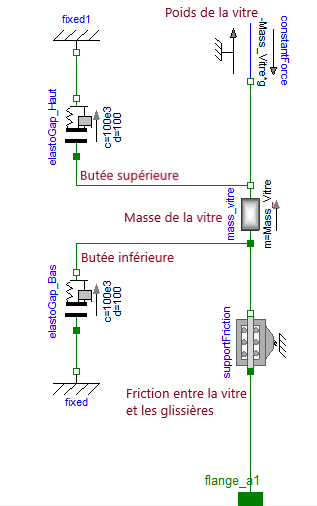
4) Dans le mécanisme du lève vitre, donnez les principaux effets transformateurs et les équations les plus simples permettant de les prendre en compte
Les effets transformateurs sont les suivants:
- Moteur électrique : passage de tension ($E$) / courant ($I$) à vitesse de rotation ($\Omega$) / couple ($C$) : $C=kI$ et $E=k\Omega$
- Roue et vis sans fin : passage de vitesse de rotation/couple à vitesse de rotation/couple avec un rapport de réduction (diminution de la vitesse, augmentation du couple) : $N=\Omega_1/\Omega_2 = C_2/C_1$
- Ensemble pignon/roue : passage de vitesse de rotation/couple à vitesse de rotation/couple avec un rapport de réduction (diminution de la vitesse, augmentation du couple) : $N=\Omega_1/\Omega_2 = C_2/C_1$
- Mécanisme à ciseaux : passage de vitesse de rotation/couple à vitesse de translation/effort : $L_{arm}=v/\Omega=C/F$
5.3. Questions à choix multiples sur la modélisation de composants technologiques
1) Faites le lien entre les effets et les différents éléments du schéma :
Transformateur parfait : d
Pertes Joules dans le cuivre : a
Magnétisation du circuit magnétique : c
Le couplage imparfait du primaire et du secondaire (flux de fuite) : b
Pertes fer du circuit magnétiques : e
2) Cochez le schéma Modelica correspondant le mieux à ce composant :
Réponse : b
3) a) Le modèle représente ici des déplacements :
Verticaux
3) b) Liez les effets aux éléments du schéma
Amortisseur : c (partie frottement visqueux)
Ressort hélicoïdal : c (partie ressort)
Pneu : e
Caisse véhicule (poids) : a
Caisse véhicule (inertie) : b
Jante de la roue (inertie) : d
Position de la route : f
Le poids de la jante aurait pu être pris en compte par une source d’effort supplémentaire connectée sur la masse d.