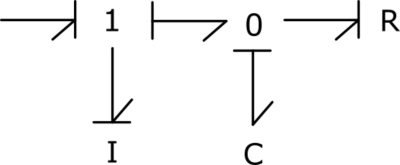Chapitre 4 : Simulation numérique de systèmes multi-physiques
5.1. Révision des différentes méthodes de modélisation
5.1.1. Le domaine électrique
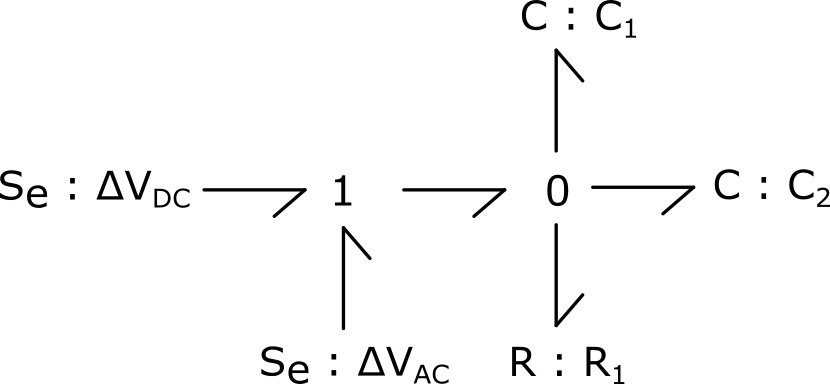
1) Modéliser le système en utilisant le formalisme bond graph :
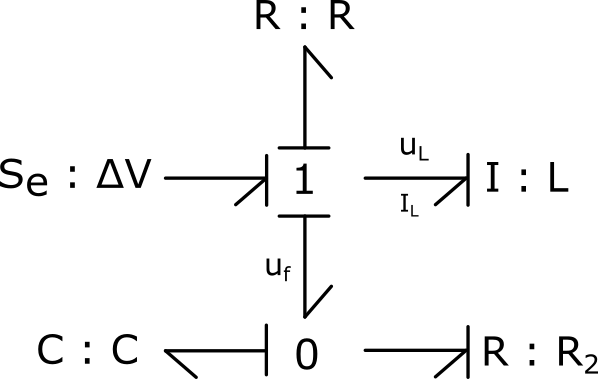
2) Déterminer le modèle schéma blocs du circuit :
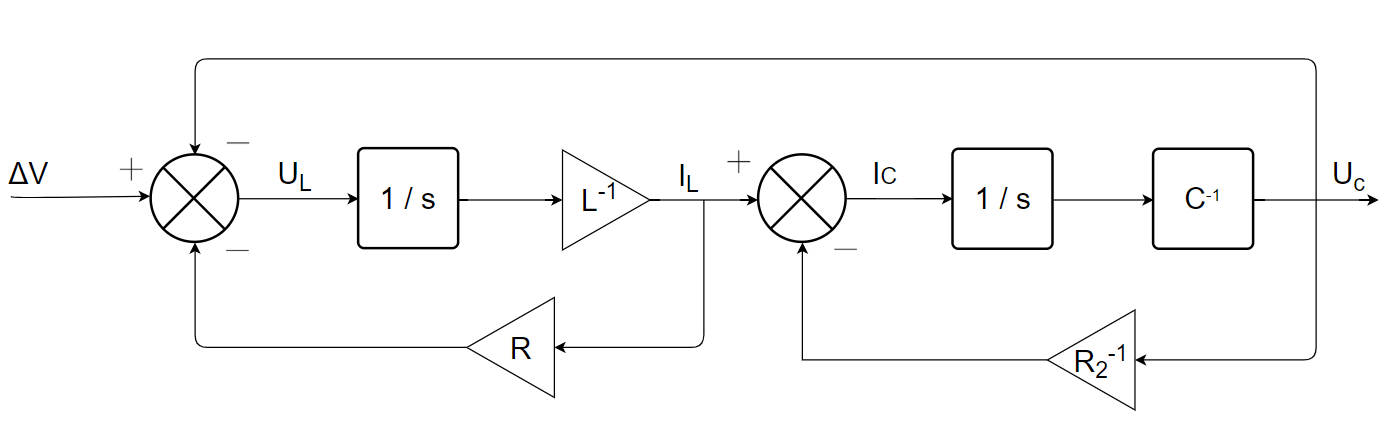
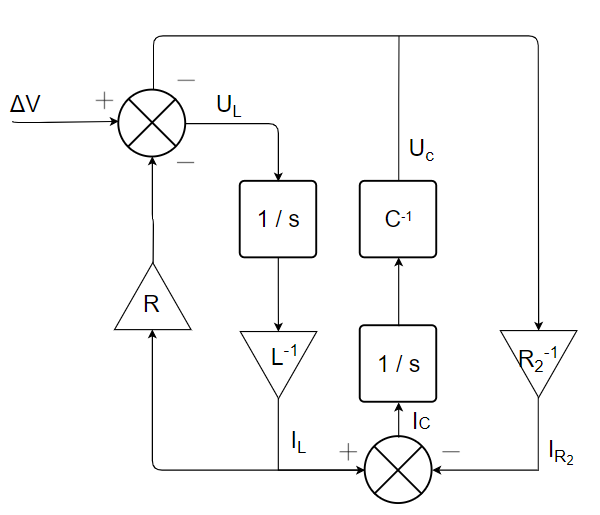
3) Obtenir la représentation d’état du système :
\begin{gather} \begin{bmatrix} \dot U_C \\ \dot I_L \end{bmatrix} = \begin{bmatrix} -R_2^{-1}.C^{-1} & C^{-1}\\ L^{-1} & R.L^{-1} \end{bmatrix} \begin{bmatrix} U_C \\ I_L \end{bmatrix} + \begin{bmatrix} 0 \\ -L^{-1} \end{bmatrix}.\Delta V \end{gather}
5.1.2. Le domaine mécanique
Non corrigé.
5.2. Études de causalité et modifications associées
5.2.1. Deux condensateurs en parallèle
1) Modéliser, en utilisant le formalisme bond graph, le système à l’étude – en ne considérant que l’effet capacitif des condensateurs.
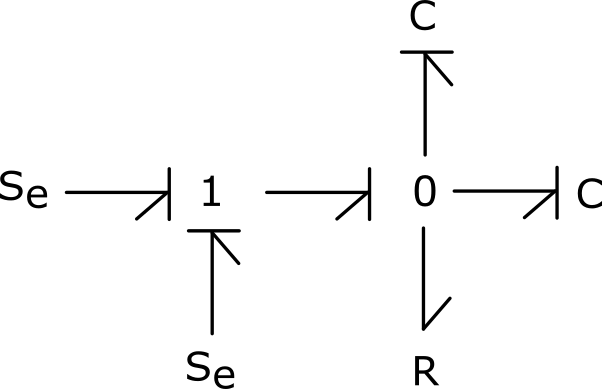
2) Attribuer les causalités du système modélisé. Est-il possible d’obtenir la causalité intégrale pour les deux condensateurs ?
Non c’est impossible.
3) Dans la pratique, un condensateur possède des résistance et inductance internes. Ces éléments sont à modéliser tous deux en série de l’effet capacitif. Mettre à jour le modèle bond graph en considérant ces phénomènes physiques et conclure sur le sens physique de cette modélisation en attribuant les causalités.
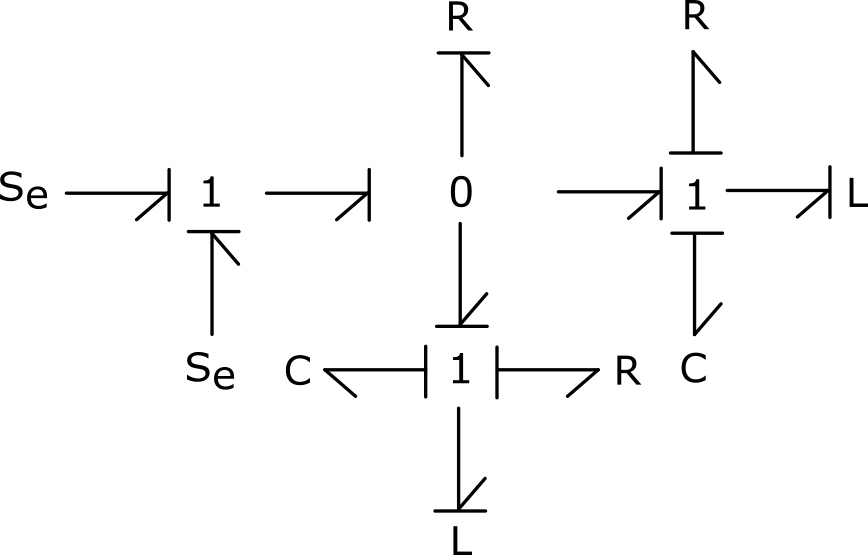
L’ajout de ces effets/phénomènes physiques permet l’obtention des causalités intégrales du modèle.
5.2.2. Les inerties de système de propulsion d’un sous-marin
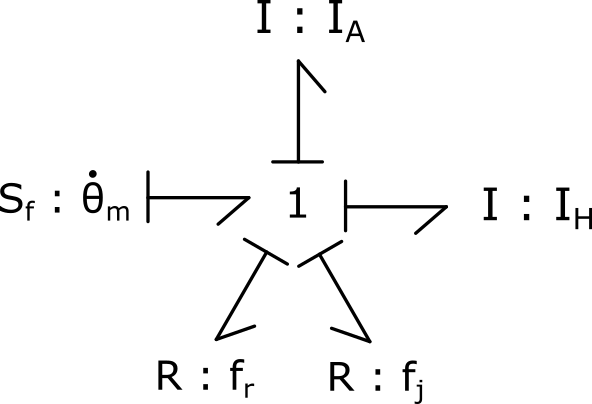
1) En considérant le moteur électrique comme une source de vitesse idéale, proposer une modélisation bond graph incluant les phénomènes physiques suivants : frottements du roulement et du joint d’étanchéité et les inerties de l’arbre et de l’hélice.
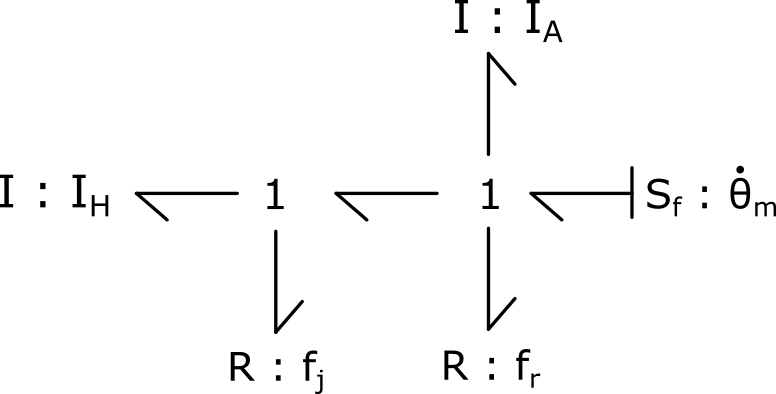
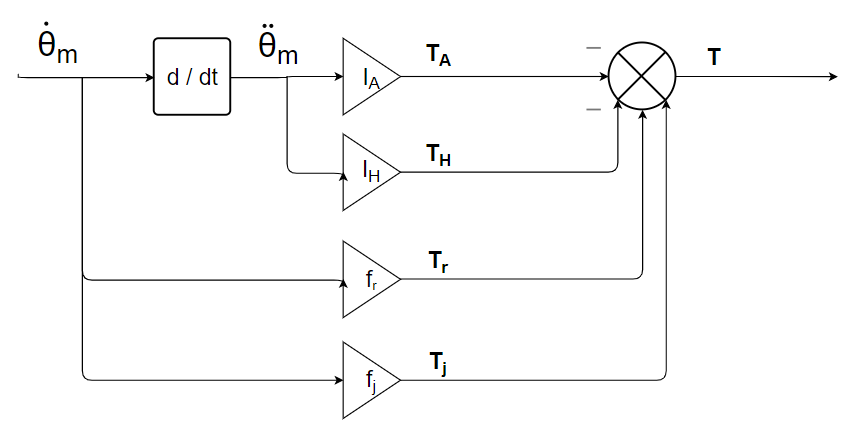
2) Attribuer les causalités au modèle bond graph et implémenter le modèle schéma bloc associé.
4) Introduire la raideur de l’arbre, détaillée dans le tableau 3.8, entre les inerties et le moteur électrique. Combien d’inerties sont en causalité dérivée ?
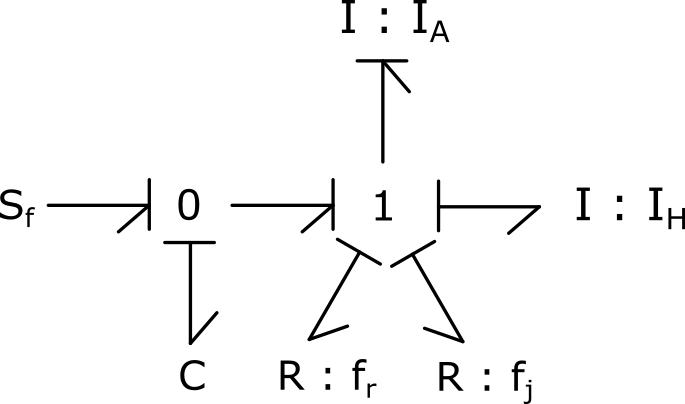
Il reste une inertie en causalité dérivée.
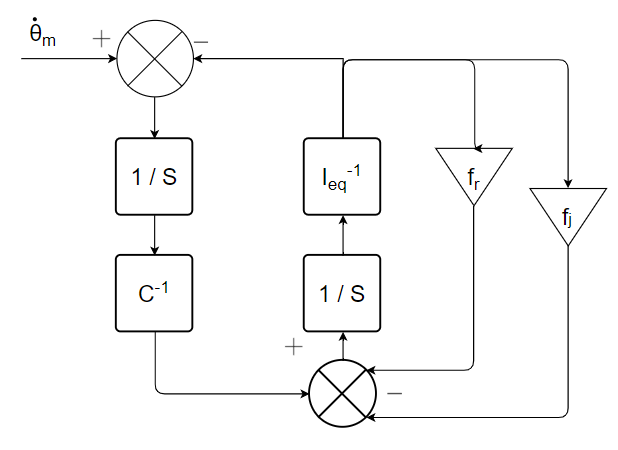
5) Remplacer les deux inerties par une unique inertie équivalente. Déterminer le schéma bloc du système modélisé. Conclure sur les causalités préférentielles du modèle.
6) Proposer une autre méthode permettant l’élimination des causalités dérivées.
Il serait, par exemple, possible de considérer une raideur entre l’arbre et l’hélice.
5.2.3. Contrainte de causalité : le frottement sec
1) Appliquer la causalité flux à l’élément R du bond graph 4.19.a et propager les causalités au modèle, en favorisant les causalités préférentielles autant que faire se peut. Discuter le comportement du modèle de friction autour d’une vitesse nulle.
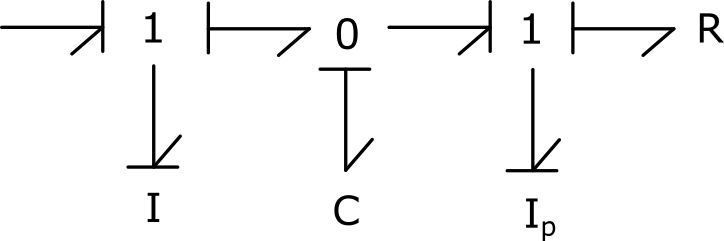
L’élément C est en causalité dérivée.
2) Afin d’obtenir une causalité intégrale sur l’élément C, proposer deux nouveaux modèles causaux :
1)
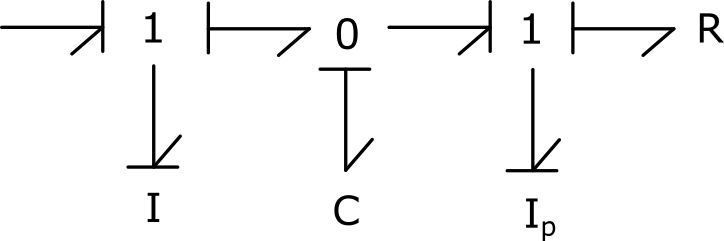
2) Si la caractéristique de R est irréversible, il n’est plus nécessaire de l’avoir en causalité flux. On peut donc avoir le modèle suivant :